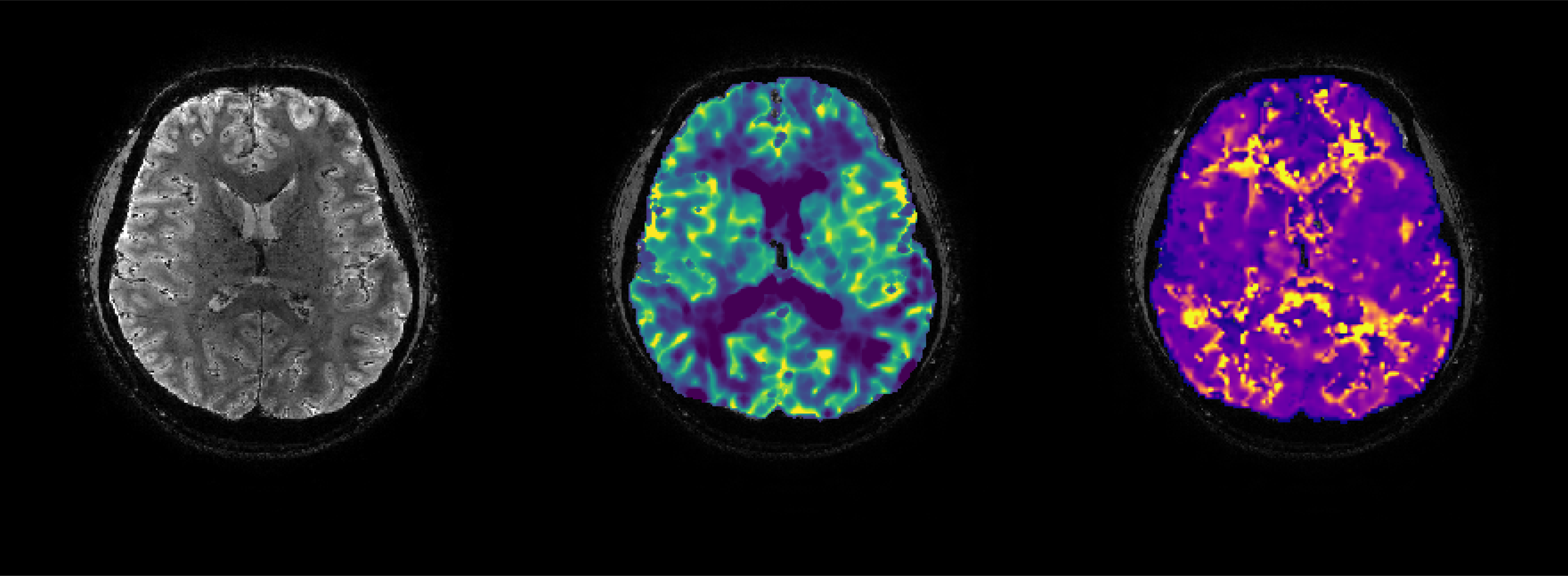
The test data for this tutorial consists of a pre-processed BOLD dataset acquired using a 7 tesla Philips MRI system. The volunteer was instructed to perform 3 consecutive breath-hold periods in order to evoke a CVR response. Simply unzip the test data file and update the data path (/Data) pointing to the image files along with the sequence path (/Data/traces) in the included Matlab demo file (.mlx). Note the effect of including nuisance variables in the lag calculation! … and always download the latest code from the Github page.
TUTORIAL 2: CVR mapping without respiratory challenges: i.e. using breath-holding or just a simple resting-state fMRI scan
This tutorial comprises a template data analysis script that utilizes native matlab functions as well as functions from the seeVR toolbox. If you use any part of this process or functions from this toolbox in your work please cite the following article:
Bhogal AA.,Medullary vein architecture modulates the white matter BOLD cerebrovascular reactivity signal response to CO2: observations from high-resolution T2* weighted imaging at 7T. Neuroimage 15 Dec, 2021. Vol 245, https://doi.org/10.1016/j.neuroimage.2021.118771
... and toolbox
Alex A. Bhogal, (2023). abhogal-lab/seeVR: 1.53 (v1.53). Zenodo. https://doi.org/10.5281/zenodo.7816690
If you have suggestions for improvement or find bugs, please contact me at a.bhogal@umcutrecht.nl, https://www.seevr.nl/contact-collaboration/ or feel free to start a new branch at https://github.com/abhogal-lab/seeVR
************************************************************************************************************************************
loadTimeseries: wrapper function to load nifti timeseries data
loadMask: wrapper function to load associated masks
meanTimeseries: calculates the average time-series signal intensity in a specific ROI
demeanData: subtracts the mean value from each voxel time-series
normTimeseries: normalizes time-series data to a specified baseline period
remLV: generates a mask that can be used to isolate and remove large vessel signal contributions
filterData: perfomes gaussian smoothing operation on image/time-series data
glmCVRidx: uses a general linear model approach to calculate a 'CVR index' - suitable when CO2 data is not available
lagCVR: calculates CVR and hemodynamic lag using a cross-correlation or lagged-GLM approach
*************************************************************************************************************
MRI Data Properties
This example uses BOLD data acquired using a Philips 7 tesla MRI scanner with the
following parameters:
Scan resolution (x, y): 112 109
Scan mode: MS
Repetition time [ms]: 1700
Echo time [ms]: 25
FOV (ap,fh,rl) [mm]: 224 59.2 224
Scan Duration [sec]: 281
Slices: 27
Volumes: 160
EPI factor: 37
Slice thickness: 2mm
Slice gap: 0.2mm
In-place resolution (x, y): 2mm
MRI Data Processing
Simple pre-processing of MRI data was done using FSL (https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/) as follows
1) motion correction (MCFLIRT)
2) calculate mean image (FSLMATHS -Tmean)
3) brain extraction (BET f = 0.2 -m)
4) tissue segmentation on BOLD image (FAST -t 2 -n 3 -H 0.2 -I 6 -l 20.0 -g --nopve)
Analysis Pipeline
1: Setup options structure and load data
The seeVR functions share parameters using the 'opts' structure. In the current version this is implemented as a global variable (subect to change in the future). To get started, first initialize the global opts struct. Nifti data can be loaded using the loadTimeseries/LoadMask wrapper functions based on the native matlab nifti functions (or 'loadImageData' using provided nifti functions - see which one works for you). This function will also initialize certain variables in the opts structure including opts.TR (repetition time). opts.dyn (number of volumes), opts.voxelsize (resolution), and opts.info ( if using loadTimeseries then opts.headers is initialized and used by saveImageData to save timeseries, parameter maps and masks in opts.headers.ts/map/mask).
*If you use your own functions to load your imaging data, ensure that you also fill the above fields in the opts structure to ensure maintained functionality (especially opts.TR). If functions throw errors, it is usually because a necessary option is not specified before the function call.
Startup - use 'ctrl + enter' to run individual code blocks
clear all
clear global all
close all
% initialize the opts structure (!)
global opts
opts.verbose = 0;
% Set the location for the MRI data
datadir = 'ADDPATH to DATA\';
cd(datadir)
% Load motion corrected data
filename = 'BOLD_masked_mcf.nii.gz';
[BOLD,INFO] = loadTimeseries(datadir, filename);
% Load GM segmentation
file = 'BOLD_mean_brain_seg_0.nii.gz';
[GMmask,INFOmask] = loadMask(datadir, file);
% Load WM segmentation
file = 'BOLD_mean_brain_seg_1.nii.gz';
[WMmask,~] = loadMask(datadir, file);
% Load CSF segmentation
file = 'BOLD_mean_brain_seg_2.nii.gz';
[CSFmask,~] = loadMask(datadir, file);
% Load brain mask
file = 'BOLD_mean_brain_mask.nii.gz';
[WBmask,~] = loadMask(datadir, file);
2: Setup directories for saving output
Pay special attention to the savedir, resultsdir and figdir as you can use these to organize the various script outputs.
Setup necessary directories
% specify the root directory to save results
opts.savedir = datadir;
% specify a sub directory to save parameter maps - this
% directory can be changed for multiple runs etc.
opts.resultsdir = fullfile(datadir,'RESULTS'); mkdir(opts.resultsdir);
% specify a sub directory to save certain figures - this
% directory can be changed for multiple runs etc.
opts.figdir = fullfile(datadir,'FIGURES'); mkdir(opts.figdir);
3: Take a quick look at the data
Use the 'meanTimeseries' function with any mask to look at the ROI timeseries. To see the differences between GM, WM and whole-brain timeseries, use the 'demeanData' function before plotting. We can also use the 'normTimesieres' function to normalize the BOLD data and look at the %BOLD signal change relative to the baseline period. There are two ways to do this: 1) specify the baseline start and end indexes; 2) select the baseline start and end points.
Visualize ROI timeseries
figure;
TS1 = meanTimeseries(BOLD, GMmask);
TS1 = demeanData(TS1);
% Plot GM timeseries
plot(TS1, 'k'); title('3X inspiratory breath-hold');
xlabel('absolute signal'); ylabel('time (s)'); xlim([0 length(TS1)]);
% Overlay WM timeseries
hold on
TS2 = meanTimeseries(BOLD, WMmask);
TS2 = demeanData(TS2);
plot(TS2, 'c');
title('3X inspiratory breath-hold'); xlim([0 length(TS1)]);
% Overlay WB timeseries
TS3 = meanTimeseries(BOLD, WBmask);
TS3 = demeanData(TS3);
plot(TS3, 'm');
title('3X inspiratory breath-hold'); xlim([0 length(TS1)]);
legend('GM','WM', 'WB')
hold off
clear TS1 TS2 TS3
4: Removing contributions from large vessels
CVR data can often be weighted by contributions from large vessels that may overshadow signals of interest. Particulary, for very high resolution acquisitions at high field strength. We can modify the whole brain mask to exclude large vessel contributions using the 'remLV' function ('remove large vessels'). This can be done by specifying the percentile threshold from which to remove voxels, or if the appropriate toolbox is not available, a manual threshold value. If this function fails, try restarting fromt step 1 and loading all data using loadImageData.m function.
Remove large vessel contributions
% Supply necessary options
% Define the cutoff percentile (higher values are removed; default = 98);
opts.LVpercentile = 99;
% If the stats toolbox is not present, then a manual threshold must
% be applied. This can vary depending on the data (i.e. trial and error).
opts.verbose = 1;
[mWBmask] = remLV(BOLD,WBmask,opts);
5: Smooth and normalize data
There are several tunable smoothing options ranging from standard gaussian to edge-preserving bilateral smoothing. For MAC users (sorry) this is restricted to gaussian but you can easily replace with your own spatial smoothing algorithms.
Spatial smoothing
% 'guided' gaussian smoothing (for MAC see smthData function)
opts.filter = 'gaussian';
opts.spatialdim = 3; %default = 2
opts.FWHM = [5 5 5];
% Normalize data to first 15 baseline images. *NB if nornIdx is not
% supplied, you will be asked to manually select baseline indices.
normIdx = [1 15];
nBOLD = normTimeseries(BOLD,mWBmask,normIdx);
%use modified mask from step 5 as input to avoid smoothing large vessel
%signals into tissues
guideImg = squeeze(BOLD(:,:,:,1));
sBOLD = filterData(nBOLD, guideImg, mWBmask, opts);
clear nBOLD
6: Estimating relative CVR
In a perfect world we would have some idea of arterial gas tensions to which we could relate our BOLD signal changes. This would allow us to normalized our data and express signal changes as a function of changes in mmHg of CO2 or O2. For simple BH experiments this is often not the case - due to the need for gas monitoring systems etc. In cases where gas traces are not available, relative CVR maps can be generated using the 'glmCVRidx' function. This functions uses a reference signal (i.e. from a GM, cerebelum or saggital sinus mask) as a explanatory variable and outputs a parameter map of beta values that can be interpreted as the relative CVR response. Signals are first band-pass filtered using the frequency range specified in the opts.fpass parameter. The function returns the CVRidx map, the band passed reference signal used for normalization and the band-passed BOLD timeseries if specified. Resulting maps are saved in opts.resultsdir\CVRidx\. NB this function can also be used to estimate CVR from resting state fMRI. In this case the vascular response is estimated based on low frequency oscillations. If using resting state data, it might be informative to explore different frequency limits for opts.fpass.
Often, breath-hold data can be somewhat corrupted due to motion artefacts. Imagine a subect is instructed to do an inspiratory BH (considered more tolerable than expiratory BH), when they inhale, the lungs expand and this can lead to tilting of the head. This motion can lead to artefacts in our BOLD signal that correlate with our BH task. We can examine the motion parameters and see if it is worthwhile to regress them out from our BOLD data. One of the strengths of the seeVR functions is the ability to play with explanatory regressors and nuissance regressors. In the current seeVR version, handling of nuissance signals has been integrated in the glmCVRidx function.
Calculate relative CVR considering motion parameters
% to calculate CVR, nuissance regressors can now be supplied.
% ** note, this function can also output band-passed signals
% ** note, here we supply the GMmask as an ROI to generate the reference
% signal but you can supply any mask (for example, cerebellum or CSF or a
% saggital sinus mask etc.)
% load nuisance signals
% load nuisance signals
cd(datadir) % Go to our data directory
mpfilename = 'BOLD_mcf.par'; % Find MCFLIRT motion parameter file
nuisance = load(mpfilename); % Load nuisance regressors (translation, rotation etc.)
% Calculate motion derivatives
dtnuisance = gradient(nuisance); % temporal derivative
sqnuisance = nuisance.*nuisance; % square of motion
motion = [nuisance dtnuisance sqnuisance];
drift_term = 1:1:size(sBOLD,4);
%concatenate motion params with drift term
np = [motion drift_term'];
% rescale regressors
for ii=1:(size(np,2)); np(:,ii) = rescale(np(:,ii),-1, 1); end
opts.fpass = [0.000001 0.1164]; % accept a wide frequency band (for LFO you can set this to 0.0001 --> 0.08 for example
[CVRidx_maps, ~, ~] = glmCVRidx(sBOLD, mWBmask, GMmask, np, opts);
% and now without nuisance regression
[CVRidx_maps2, ~,~] = glmCVRidx(sBOLD, WBmask, GMmask, [], opts);
This approach outlined above can also be used to generate CVR maps from resting-state fMRI data!
7: Calculating Hemodynamic Lag
In addition to CVR, hemodynamic lag can be another interesting parameter to consider when looking at vascular impairment. A common approach to doing this involves performing a cross-correlation or lagged-GLM approach with some stimulus waveform (PetCO2 or PetO2). The calculated lags with respect to this waveform probe are then plotted voxel-wise to produce a lag parameter map. A more advanced approach is to use this input probe in order to generate an optimized regressor (see: https://rapidtide.readthedocs.io/en/stable/). This analysis technique has also been implemented in the seeVR toolbox in the 'lagCVR' function. This function is capable of generating an optimized BOLD regressor, lag maps based on both a cross-correlation and/or lagged-GLM analysis, CVR maps as well as many statistical maps to evaluate analysis outputs. Since we do not have any breathing traces in this example, we will use the signal as a probe through which to select highly correlated voxels that will comprise the optimized BOLD regressor. Furthermore, we will skip generating CVR maps (lagCVR performs linear regression of the BOLD signal against the end-tidal trace to generate CVR/O2-resonse maps) - we've anyways already created the CVR index maps in step 5. As input, use the band-passed signals obtained using glmCVRidx above.
Calculating hemodynamic lag using the GLM with nuisance parameters
% The lagCVR function has many options and possible outputs; some of which
% more useful than others. For details, look at default options in the .m file.
% For BH data, motion can be a problem when estimating lag. So we will chose the slower, more memory
% intensive GLM so that we can take into acount nuisance signals. Maps are
% compared in the plotting section below
opts.glm_model = 1;
opts.corr_model = 1;
% since we already generated CVR maps, we can skip that step here and focus
% on lag only
opts.cvr_maps = 0; %default = 1
% Produces the optimized regressor (default = 1). When this is set to 0; a straight correlation
% with the input probe is done. Since our input signal is BOLD-based, the
% effect of this step should be negligeable
opts.refine_regressor = 1; %default = 1
% Factor by which to temporally interpolate data. Better for picking up
% lags between TR. Higher value means longer processing time and more RAM
% used (so be careful) - set to 1 for fastest results!
opts.interp_factor = 1; %default is 4
% The correlation threshold is an important parameter for generating the
% optimized regressor. For noisy data, a too low value will throw an error.
% Ideally this should be set as high as possible, but may need some trial
% and error.
opts.corr_thresh = 0.7; %default is 0.7
% Thresholds for refinening optimized regressors. If you make this range too large
% it smears out your regressor and lag resolution is lost. When using a CO2
% probe, the initial 'bulk' alignment becomes important here as well. A bad
% alignment will mean this range is also maybe not appropriate or should be
% widened for best results. Since we use the actual BOLD as a probe we keep
% this range tight.
opts.lowerlagthresh = -3; %default is -3
opts.upperlagthresh = 3; %default is 3
% Lag thresholds for lag map creation. Since we are looking at a healthy
% brain, this can be limited to between 20-60TRs. For impariment you can consider
% to raise the opper threshold to between 60-90TRs. (ASSUMING TR ~1s!, careful).
opts.lowlag = -5; %setup lower lag limit; negative for misalignment and noisy correlation
opts.highlag = 40; %setups upper lag limit; allow for long lags associated with pathology
probe = meanTimeseries(sBOLD, GMmask); % reference signal
[optimized_probe, maps] = lagCVR(GMmask,mWBmask,sBOLD,probe,nuisance,opts);
rmse = 0.5676
rmse = 0.0062
rmse = 6.1493e-04
passes = 1
perc = 0.0964
passes = 1
perc = 0.0723
% The advantage of using the global opts struct is that the variables used
% for a particular processing run (including all defaults set within
% functions themselves) can be saved to compare between runs.
save([opts.resultsdir,'processing_options.mat'], 'opts');
8: Plot Results
Compare CVR with and without nuisance
%setup options
opts.scale = [-2 2]; % this is the expected data range. Default is [-5 5]
opts.row = 4; % this is the nr of rows. More rows means more images. Too many images will throw an error
opts.col = 6; % this is the nr of columns. This should be an even number. For 6 cols, 3 will be source images and 3 will be the param map.
opts.step = 1; % This value is multiplied by 2 in the function. So step = 2 means you jump 4 slices between images.
opts.start = 2; % this is the starting image
%PLOT NORMALIZED RELATIVE CVR WITH NUISANCE REGRESSION
sourceImg = imrotate(squeeze(BOLD(:,:,:,1)),90); %use the guide image we used for smoothing. Alternatively a mean BOLD image or single time-point
paramMap1 = imrotate(CVRidx_maps.nCVRidx, 90); % use the basic CVR map calculated using LagCVR
mask = imrotate(mWBmask, 90);
map = flip(brewermap(128, 'Spectral')); %use the spectral colormap (or any other you like)
%map = BWR2(101);
%generate plots
plotMap(sourceImg,mask,paramMap1,map,opts);
%PLOT NORMALIZED RELATIVE CVR WITHOUT NUISANCE REGRESSION
paramMap2 = imrotate(CVRidx_maps2.nCVRidx, 90);
plotMap(sourceImg,mask,paramMap2,map,opts);
%PLOT difference
opts.scale = [-0.2 0.2];
map = BWR(51);
plotMap(sourceImg,mask,(paramMap2 - paramMap1),map,opts);
Compare LAG with and without nuisance (huge improvement when using nuisance signals!)
%PLOT HEMODYNAMIC LAG MAP USING OPTIMIZED BOLD REGRESSOR AND NUISANCE
%SIGNALS (GLM MODEL)
paramMap = imrotate(maps.GLM.optiReg_lags, 90); % use the basic CVR map calculated using LagCVR
opts.scale = [0 50];
%update colormap
map = plasma(50);
%plot map
plotMap(sourceImg,mask,paramMap,map,opts);
%PLOT HEMODYNAMIC LAG MAP USING OPTIMIZED BOLD REGRESSOR WITHOUT NUISANCE
%SIGNALS (XCORR MODEL)
paramMap = imrotate(maps.XCORR.lag_opti, 90); % use the basic CVR map calculated using LagCVR
%plot map
plotMap(sourceImg,mask,paramMap,map,opts);
